最近在参加比赛，直面了许多特征处理相关的问题，一个比赛or项目不光要求对模型算法有好的理解，还对手上仅有的数据有很高的处理要求。
找出了手头有的《精通特征工程》有针对性看了几张跟数据挖掘相关的内容，整理思维导图如下。

比赛介绍

数据集

本数据集来源于DC竞赛平台。数据主要包括影响员工离职的各种因素（工资、出差、工作环境满意度、工作投入度、是否加班、是否升职、工资提升比例等）以及员工是否已经离职的对应记录。

其中训练数据主要包括1100条记录，31个字段，测试数据主要包括350条记录，30个字段，测试数据不包括员工是否已经离职的记录，要求使用逻辑回归等对员工离职进行预测。（注：比赛所用到的数据取自于IBM Watson Analytics分析平台分享的样例数据。该平台只选取了其中的子集，并对数据做了一些预处理使数据更加符合逻辑回归分析比赛的要求。）

评测标准

使用混淆矩阵来评价模型的准确率acc。
acc = （TP+TN)/(TP+FP+FN+TN)

数据分析和预处理

首先观察数据类型train.info()、test.info()。可以看到既有int也有object，要对他们进行分别处理。当然，有时候int其实也代表着离散变量，可当作object处理。

1

train.describe()

查看数字型参数。其中，EmployeeNumber列是没有意义的参数，可以删去。同时，可以发现Over18和StandardHours中的元素全部相同，也删去。

1
2
3
4
5
6
7
8

train['Over18'].unique() # 输出array(['Y'], dtype=object)，只含一种元素，'StandardHours'同理
# 对训练集和测试集一起进行数据处理
test['Attrition']=-1
data = train.append(test).reset_index(drop=True) # data即为训练集+测试集
# 删除没有意义的列
data.drop(['Over18', 'StandardHours','EmployeeNumber'], axis=1, inplace=True) 
# 筛选出类别特征
feat_col = [i for i in data.select_dtypes(object).columns if i not in ['Attrition']]

可以看到现在的object列为['BusinessTravel', 'Department', 'EducationField', 'Gender', 'JobRole', 'MaritalStatus', 'OverTime']。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 自定义one-hot
def encode_onehot(df,column_name):
    feature_df=pd.get_dummies(df[column_name], prefix=column_name)
    all_col = pd.concat([df.drop([column_name], axis=1),feature_df], axis=1)
    return all_col
# 对类别特征进行one-hot 
for i in cat_col:
    data = encode_onehot(data,i)
# 使用LR需要对所有参数进行归一化
max_min_scaler = lambda x : (x-np.min(x))/(np.max(x)-np.min(x))
for i in feats:
    data[i]=data[[i]].apply(max_min_scaler)
    
data.isnull().sum() # 确认数据没有空值

此时再打印data可以看到所有数据都被转化成了[0,1]之间的浮点数。

建模及预测

1
2
3
4
5
6
7
8
9
10

# 重新分割出train和test
X_train = data[data['Attrition'] !=-1][feats]
y_train = data[data['Attrition'] !=-1]['Attrition']
X_test = data[data['Attrition'] ==-1][feats]
# 训练模型
lr_model = LogisticRegression()
lr_model.fit(X_train,y_train)
pre = lr_pre.predict(X_test)
result = pd.DataFrame({'result':pre.astype(int)}) # 比赛要求整型
result.to_csv(path+'output/new_lr',index=False)

逻辑回归单个模型simple版得分0.89428。可以做更进一步的分析处理。

进一步提升

之前也简单写过数据清洗和特征工程对于一个模型的优劣有着重要的影响，下面就来看一下效果。

Solution1：特征提取

1
2
3
4
5
6
7
8
9

# 绘制特征相关性图
corr = data.corr()
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use({'figure.figsize':(10,8)})

sns.heatmap(corr, xticklabels=corr.columns.values, yticklabels=corr.columns.values,cmap="YlGnBu")
plt.show()

可以看到MonthlyIncome和JobLevel高度相关，TotalWorkingYears和多个特征都较相关，故尝试删除JobLevel和TotalWorkingYears。

Solution2：交叉验证

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sklearn.model_selection import KFold
model=LogisticRegression()
n_splits=5
kfold = KFold(n_splits=5, shuffle=True, random_state=42)
res['pred'] = 0
model.random_state = 42
for train_idx, val_idx in kfold.split(X_train):
    model.random_state = model.random_state + 1
    train_x1 = X_train.loc[train_idx]
    train_y1 = y_train.loc[train_idx]
    test_x1 = X_train.loc[val_idx]
    test_y1 = y_train.loc[val_idx]
    model.fit(train_x1, train_y1) 
    result = model.predict(X_test)

结合Solution1和2得分为0.905714（96/2816）。

Solution3：模型融合

突然发现XGBoost好像不能算是基本算法，不过也姑且整理再这里了。本文梳理了陈天奇Introduction to Boosted Trees的slides，有些长。

背景

需要的预备知识：CART回归树算法，梯度下降法及泰勒公式。
看预备知识就可以知道，XGBoost（eXtreme Gradient Boosting）由GBDT发展而来，是一种基于树模型的集成算法。目前在各大比赛场上斩杀无数算法，可以说是是数据挖掘比赛必备。

算法简述

陈天奇的slides对于算法的解释十分详细，简述基于PPT。

Review of key concepts of supervised learning | 回顾监督学习的关键概念

• Model|模型：如何用xi来预测yi_hat。对于线性模型来说，预测值yi_hat基于不同的任务有不同的计算。
• Parameters|参数：从数据中学得。
• Objective function|目标函数：由训练误差（损失函数）training loss和正则化项Regularization组成。训练误差有平方误差和交叉熵损失函数；正则化项有L1和L2。
  其中，线性回归模型加L2正则是Ridge regression，线性回归模型加L1正则是Lasso，逻辑回归模型加L2正则。
• The conceptual separation between model, parameter, objective also gives you engineering benefits。
  • 损失函数表示模型对训练数据的拟合程度，loss越小，代表模型预测的越准，即偏差Bias越小。
  • 正则化项衡量模型的复杂度，regularization越小，代表模型模型的复杂度越低，即方差Variance越小。
  • 目标函数越小，代表模型越好。Bias-variance tradeoff也是一个模型能力的体现。

Regression Tree and Ensemble (What are we Learning)

关于树模型集成方法Tree Ensemble methods：

• Very widely used, look for GBM, random forest…
  被广泛使用
  • Almost half of data mining competition are won by using some variants of tree ensemble methods
    接近半数数据挖掘比赛冠军队使用树集成方法
• Invariant to scaling of inputs, so you do not need to do careful features normalization.
  和输入数据的取值范围无关，所以无需做很细致的特征归一化
• Learn higher order interaction between features.
  能学习到高位特征的相关性
• Can be scalable, and are used in Industry
  扩展性好，工业使用

• yi_hat由所有树模型决定，模型复杂度space of function包含所有回归树。
• 不学习权重， 而是学习function，即fK（tree）。

• 决策树具有启发式思想。用信息增益决定分裂节点，减少损失。
• 树的剪枝，最大深度以及叶节点权重都会影响模型复杂度。对树进行剪枝，对叶节点的权重进行L2正则化能减少模型复杂度，提高模型稳定性。
• 回归树不仅可以解决回归问题，还能做分类、排序问题，这取决于你的目标函数。例如平方误差和交叉熵损失函数。

Gradient Boosting (How do we Learn)

• Bias-variance tradeoff is everywhere
  偏差方差均衡无处不在
• The loss + regularization objective pattern applies for regression tree learning (function learning)
  损失函数+正则的目标函数模式适用于回归树的学习
• We want predictive and simple functions
  我们需要泛化能力强又简单的模型（奥卡姆剃刀原则）

来求解优化一下目标函数，感受一下算法的精华。
和一般Boosting方法一样，采用加性模型，并考虑平方差损失，引入泰勒展开来近似损失。（嗯，可以掏出小本本算一算了）

于是，得到了新的目标函数Obj = 损失函数+正则项+常数项。

Why spending s much efforts to derive the objective, why not just grow trees …
为什么花这么多时间去分解目标函数，而不是单纯使树增长

• Theoretical benefit: know what we are learning, convergence
  理论优势：能知道模型在学什么
• Engineering benefit: recall the elements of supervised learning
  工程优势：回顾一下监督学习的元素
  • gi and hi comes from definition of loss function
    gi和hi由损失函数的定义而来
  • The learning of function only depend on the objective via gi and hi
    需要学习的函数只取决于gi和hi
  • Think of how you can separate modules of your code when you are asked to implement boosted tree for both square loss and logistic loss

Summary

参数说明

原始函数

Before running XGBoost, we must set three types of parameters: general parameters, booster parameters and task parameters.

• General parameters relate to which booster we are using to do boosting, commonly tree or linear model
• Booster parameters depend on which booster you have chosen
• Learning task parameters decide on the learning scenario. For example, regression tasks may use different parameters with ranking tasks.
• Command line parameters relate to behavior of CLI version of XGBoost.
  具体参数详见XGBoost官方文档。

Python API

Python API官方文档
括号内为 sklearn 参数。

通用参数

• booster：基学习器类型，gbtree，gblinear 或 dart（增加了 Dropout） ，gbtree 和 dart 使用基于树的模型，而 gblinear 使用线性模型
• silent：使用 0 会打印更多信息
• nthread：运行时线程数

Booster 参数

树模型Tree booster

• eta（learning_rate）：更新过程中用到的收缩步长，[0, 1]。
• gamma：在节点分裂时，只有在分裂后损失函数的值下降了，才会分裂这个节点。Gamma 指定了节点分裂所需的最小损失函数下降值。这个参数值越大，算法越保守。
• max_depth：树的最大深度，这个值也是用来避免过拟合的
• min_child_weight：决定最小叶子节点样本权重和。当它的值较大时，可以避免模型学习到局部的特殊样本。但如果这个值过高，会导致欠拟合。
• max_delta_step：这参数限制每颗树权重改变的最大步长。如果是0意味着没有约束。如果是正值那么这个算法会更保守，通常不需要设置。
• subsample：这个参数控制用于每棵树随机采样的比例。减小这个参数的值算法会更加保守，避免过拟合。但是这个值设置的过小，它可能会导致欠拟合。
• colsample_bytree：用来控制每颗树随机采样的列数的占比。
• colsample_bylevel：用来控制的每一级的每一次分裂，对列数的采样的占比。
• lambda（reg_lambda）：L2 正则化项的权重系数，越大模型越保守。
• alpha（reg_alpha）：L1 正则化项的权重系数，越大模型越保守。
• tree_method：树生成算法,auto, exact, approx, hist, gpu_exact, gpu_hist
• scale_pos_weight：各类样本十分不平衡时，把这个参数设置为一个正数，可以使算法更快收敛。典型值是 sum(negative cases) / sum(positive cases)

Dart 额外参数

• sample_type：采样算法
• normalize_type：标准化算法
• rate_drop：前置树的丢弃率，有多少比率的树不进入下一个迭代，[0, 1]
• one_drop：设置为 1 的话每次至少有一棵树被丢弃。
• skip_drop：跳过丢弃阶段的概率，[0, 1]，非零的 skip_drop 比 rate_drop 和 one_drop 有更高的优先级。

线性模型

• lambda（reg_lambda）：L2 正则化项的权重系数，越大模型越保守。
• alpha（reg_alpha）：L1 正则化项的权重系数，越大模型越保守。
• lambda_bias（reg_lambda_bias）：L2 正则化项的偏置。

学习任务参数

• objective：定义需要被最小化的损失函数。
• base_score：初始化预测分数，全局偏置。
• eval_metric：对于有效数据的度量方法，取值范围取决于 objective。
• seed：随机数种子，相同的种子可以复现随机结果，用于调参。

代码实现

XGB-sklearn示例官方源码

和GBDT的比较以及优点

1. 损失函数：GBDT是一阶，XGB是二阶泰勒展开
2. XGB的损失函数可以自定义，具体参考 objective 这个参数
3. XGB的目标函数进行了优化，有正则项，减少过拟合，控制模型复杂度
4. 预剪枝：预防过拟合
   • GBDT：分裂到负损失，分裂停止
   • XGB：一直分裂到指定的最大深度（max_depth），然后回过头剪枝。如某个点之后不再正值，去除这个分裂。优点是，当一个负损失(-2)后存在一个正损失(+10)，(-2+10=8>0)求和为正，保留这个分裂。
5. XGB有列抽样/column sample，借鉴随机森林，减少过拟合
6. 缺失值处理：XGB内置缺失值处理规则，用户提供一个和其它样本不同的值，作为一个参数传进去，作为缺失值取值。
   XGB在不同节点遇到缺失值采取不同处理方法，并且学习未来遇到缺失值的情况。
7. XGB内置交叉检验（CV），允许每轮boosting迭代中用交叉检验，以便获取最优 Boosting_n_round 迭代次数，可利用网格搜索grid search和交叉检验cross validation进行调参。
   GBDT使用网格搜索。
8. XGB运行速度快：data事先安排好以block形式存储，利于并行计算。在训练前，对数据排序，后面迭代中反复使用block结构。
   关于并行，不是在tree粒度上的并行，并行在特征粒度上，对特征进行Importance计算排序，也是信息增益计算，找到最佳分割点。
9. 灵活性：XGB可以深度定制每一个子分类器
10. 易用性：XGB有各种语言封装
11. 扩展性：XGB提供了分布式训练，支持Hadoop实现
12. 共同优点：
    • 当数据有噪音的时候，树Tree的算法抗噪能力更强
    • 树容易对缺失值进行处理
    • 树对分类变量Categorical feature更友好

和LGB的比较

1. XGB用贪心算法排序累加，LGB用投票采样
2. XGB 异常影响全局，LGB有筛选
3. XGB速度慢，LGB改成轻量级
4. XGB 的GPU版本比LGB快，LGB则不然
5. 分布式由XGB，很少用LGB
6. XGBoost使用按层生长(level-wise)的决策树生长策略，不断优化到最大深度；LightGBM则采用带有深度限制的按叶子节点(leaf-wise)算法。在分裂次数相同的情况下，leaf-wise可以降低更多的误差，得到更好的精度。leaf-wise的缺点在于会产生较深的决策树，产生过拟合。

Reference

陈天奇PPT
XGBoost: A Scalable Tree Boosting System原著论文
CodewithZhangyi（一个很优秀的小姐姐的博客）
GBDT、XGBoost、LightGBM的使用及参数调优

本文主要针对sklearn上能进行的特征筛选和数据清洗代码做一个简单展示。

特征选择

对特征进行选择，我们可以进行如下操作。

删除低方差特征

1
2
3
4

from sklearn.feature_selection import VarianceThreshold
X = [[0,0,1],[0,1,0],[1,0,0],[0,1,1],[0,1,0],[0,1,1]]
sel = VarianceThreshold(threshold=(.8 * (1-.8)))
sel.fit_transform(X)

此时的数组已经删除方差不满足threshold的那一列特征。

1
2
3
4
5
6

array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

用threshold筛选低方差一般选取1.5~2.0。

单变量特征选择

• SelectKBest 保留评分最高的K个特征
• SelectPercentile 保留最高得分百分比之几的特征
• 对每个特征应用常见的单变量统计测试：假阳性率（false positive rate) SelectFpr，伪发现率（false discovery rate) SelectFdr ，或者族系误差（family wise error)SelectFwe。
• GenericUnivariateSelect 允许使用可配置方法来进行单变量特征选择。它允许超参数搜索评估器来选择最好的单变量特征。
• 将得分函数作为输入，返回单变量的得分和p值（或者仅仅是SelectKBest和SelectPercentile 的分数）：
  对于回归： f_regression，mutual_inf_regression
  对于分类： chi2，f_classif，mutual_inf_classif
  这在之前的数据EDA一文中有例子。

基于树模型的特征选择

用鸢尾花数据集举例。

1
2
3
4
5
6

from sklearn.ensemble import ExtraTreesClassifier
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X,y = iris.data, iris.target
X.shape

此时X是（150，4）的数组。

1
2
3
4
5
6

clf = ExtraTreesClassifier(n_estimators=50)
clf = clf.fit(X,y)
clf.feature_importances_
model = SelectFromModel(clf, prefit=True)
X_new = model.transform(X)
X_new.shape

经过特征筛选后，X_new是（150，2）的数组。

数据预处理sklearn模块

标准化scale

• 使用sklearn.preprocessing.scale()函数

  1 2	from sklearn import preprocessing X_scale = preprocessing.scale(X)

• sklearn.preprocessing.StandardScaler类

  1 2	scaler = preprocessing.StandardScaler() X_scaled = scaler.fit_transform(X)

将特征的取值缩小到某一范围

• 缩放到0到1：

  1 2	min_max_scaler = preprocessing.MinMaxScaler() X_minMax = min_max_scaler.fit_transform(X)

• 缩放到-1到1：

  1 2	max_abs_scaler = preprocessing.MaxAbsScaler() X_maxabs = max_abs_scaler.fit_transform(X)

独热编码Encoding categorical features

• preprocessing.OrdinalEncoder()
• preprocessing.OneHotEncoder()

多项式特征Generating polynomial features poly

• 进行多项式完全交叉相乘：即X的特征从（X1, X2）转换为（1，X1， X2， X1^2， X1X2， X2^2)

  1 2 3 4 5

  import numpy as np from sklearn.preprocessing import PolynomialFeatures X = np.arange(6).reshape(3,2) poly = PolynomialFeatures(2) # 转换为2阶 poly.fit_transform(X)

• 只进行多项式不同项交叉相乘：即X的特征从（X1，X2，X3）转换为（1，X1， X2，X3， X1X2， X1X3，X2X3， X1X2X3)

  1 2 3

  X = np.arange(9).reshape(3,3) poly = PolynomialFeatures(degree=3,interaction_only=True) # 转换为3阶仅不同项交叉相乘 poly.fit_transform(X)

《算法图解》Grokking algorithms（上）

最近被斌叔推荐的一本算法入门书籍，简洁精巧地讲了十几个常用算法，“像小说一样有趣”。它使我能更轻松地理解编程中的常用算法思想，我在这里分享其中的知识点和代码，原书中使用的是python2.7，我使用的是python3.6。文中插图均为原书中的配图，生动形象，同时这本书的github链接：https://github.com/egonschiele/grokking_algorithms

这本书的第一章介绍了第一种算法——二分查找和大O表示法。大O表示法指出了算法的运行时间，算法运行时间并不以秒为单位而是从其增速的角度来衡量。在第四章中介绍了平均情况和最糟情况。

选择排序 Selection sort

数组和链表是两种基本的数据结构，本书的第二章通过选择排序来更好的理解数组。
数组在储存是必须是连续的，而链表因为使用地址指向而可以分开储存。所以，数组的读取速度很快，但插入和删除速度很慢，即如下图所示。

那么，本书的第二种算法——选择排序通过将数据从大到小或从小到大排列，运行时间即为O(n^2)。
下面是将数组元素从小到大排列的代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Finds the smallest value in an array
def findSmallest(arr):
  # Stores the smallest value
  smallest = arr[0]
  # Stores the index of the smallest value
  smallest_index = 0
  for i in range(1, len(arr)):
    if arr[i] < smallest:
      smallest_index = i
      smallest = arr[i]      
  return smallest_index

# Sort array
def selectionSort(arr):
  newArr = []
  for i in range(len(arr)):
      # Finds the smallest element in the array and adds it to the new array
      smallest = findSmallest(arr)
      newArr.append(arr.pop(smallest))
  return newArr

Input

1

print(selectionSort([5, 3, 6, 2, 10]))

Output

1

[2, 3, 5, 6, 10]

递归recusion

“如果使用循环，程序的性能可能更高；如果使用递归，程序可能更容易理解。如何选择要看什么对你来说更重要。”

递归是一种自己调用自己的函数，它易于理解，但不一定在计算性能上有优势。编写递归函数时，必须告诉它何时停止递归。因此，递归函数的组成：基线条件（base case）和递归条件（recursive case）。倒计时函数的代码示例：

1
2
3
4
5
6

def countdown(i):
	print(i)
	if i<= 1:         #base case
		return
	else:             #recursive case
		countdown(i-1)

栈

栈是一种数据结构，计算机在内部使用被称为调用栈（call stack）的栈。当你调用函数时，计算机用栈来表示为这个函数调用分配的一块内存。那么，当调用某个函数时还需调用其他函数的情况，如何理解栈？

• 调用其他函数时，当前函数暂停并处于未完成状态。
• 调用其他函数时，计算机为其分配一块内存位于该函数上，在函数调用返回后，栈顶的内存块被弹出。

使用栈虽然方便，但是储存详尽的信息可能占用大量的内存，如果调用递归函数但不小心导致它没完没了运行，则最后会因为栈溢出而终止。

快速排序Quicksort

示例为使用循环和递归完成累加：

1
2
3
4
5
6
7
8
9
10
11
12

#loop sum
def sum(arr):
  total = 0
  for x in arr:
    total += x
  return total

#recursive sum
def sum(list):
  if list == []:
    return 0
  return list[0] + sum(list[1:])

递归式解决问题的思路是一种著名的问题解决方法——分而治之（divide and conquer，D&C）。
快速排序就是一个重要的D&C算法。它通过设置基准值（pivot）后对数组进行分区（partitioning），再在分区进行相同的操作来完成。
快速排序的代码：

1
2
3
4
5
6
7
8
9
10
11
12

def quicksort(array):
    if len(array) < 2:
    # base case, arrays with 0 or 1 element are already "sorted"
        return array
    else:
        # recursive case
        pivot = array[0]
        # sub-array of all the elements less than the pivot
        less = [i for i in array[1:] if i <= pivot]
        # sub-array of all the elements greater than the pivot
        greater = [i for i in array[1:] if i > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)

快速排序算法的平均运行时间为O(n log n)，而最糟情况则为O(n^2)。下图为最佳情况，也就是平均情况。

散列表Hash tables

散列表是一种包含额外逻辑的强大的数据结构，它使用散列函数来确定元素的储存位置。Python使用的散列表实现为字典。
散列表可以用于查找、防止重复、储存缓存以缓解服务器的压力。
那么，散列表是如何储存的？
它虽然模拟映射关系，但是不可能总是将不同的键映射到数组的不同位置。当遇到冲突（collision）情况，即两个键映射到了同一个位置，就在这个位置存储一个链表。所以，一个好的散列函数将极少导致冲突，使散列表的速度不会太慢。要避免冲突，需要有：

• 较低的填装因子；
• 良好的散列函数。

广度优先搜索Breadth-first search，BFS

广度优先搜索是一种用于图的查找算法，能找出两样东西之间的最短距离。

• 图由节点和边组成，用于模拟不同的东西是如何相连的。
• 广度优先搜索采用“队列（queue）”的数据结构。和栈后进先出(Last In First Out) 的数据结构相对，是一种先进先出(First In First Out) 的数据结构。

广度优先搜索的运行时间为O（人数+边数），写作O(V+E)，其中V为顶点（vertice）数，E为边数。

• 拓扑排序可以穿建一个有序的任务列表；
• 树是图的子集，树是一种完全单向指向的图。

以上是该书的前半部分内容，后半部分待整理。

在做竞赛时，有一个厉害的模型能让我们提高分数，但除此之外，有一个不可被忽视的工作，那就是数据预处理（preprocessing）。对数据集进行数据清洗和特征工程是一个显示数据处理功力 的工作，它费时耗力且需要经验积累。一个好的预处理会使模型的效果事半功倍。
波士顿房价数据集是回归问题的经典数据集，本文用的是13列的小数据集，用Python对其进行了一些基础的数据处理和可视化操作，简单探索了数据规律和模型的应用。

数据集导入和简单观察

导入数据集后，先大致了解数据集构成、相关信息。下面是一些常规的观察操作，可以选择需要的使用。

1
2
3
4
5
6
7
8
9
10
11

#导入必要的包
import pandas as pd               # 导入Python的数据处理库pandas
import seaborn as sns             # 导入python高级数据可视化库seaborn
import matplotlib.pyplot as plt   # 导入python绘图matplotlib
%matplotlib inline 

df = pd.read_csv('boston_house_price_english.csv') #导入数据集，也可以用sklearn导入
df.head()       # 前5行
df.shape        # 行列数
df.info()		# 特征信息
df.describe()	# 数值特征的基本统计学信息，如最大值最小值方差等

特征名称及解释

• CRIM: per capita crime rate by town 每个城镇人均犯罪率
• ZN: proportion of residential land zoned for lots over 25,000 sq.ft. 超过25000平方英尺用地划为居住用地的百分比
• INDUS: proportion of non-retail business acres per town 非零售商用地百分比
• CHAS: Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) 是否靠近查尔斯河
• NOX: nitric oxides concentration (parts per 10 million) 氮氧化物浓度
• RM: average number of rooms per dwelling 住宅平均房间数目
• AGE: proportion of owner-occupied units built prior to 1940 1940年前建成自用单位比例
• DIS: weighted distances to five Boston employment centres 到5个波士顿就业服务中心的加权距离
• RAD: index of accessibility to radial highways 无障碍径向高速公路指数
• TAX: full-value property-tax rate per $10,000 每万元物业税率
• PTRATIO: pupil-teacher ratio by town 小学师生比例
• B: 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town 黑人比例指数
• LSTAT: % lower status of the population 下层经济阶层比例
• MEDV: Median value of owner-occupied homes in $1000’s 业主自住房屋中值

数据探索性分析EDA和可视化

查看缺失值

1

df.isnull().any().sum()		# 看是否有缺失值

输出是0，这份小的数据集是没有缺失值的。
当出现缺失值时，先观察缺失值比例，占比较大的列可以考虑删去。缺失值一般以三种形式存在：NA/NULL/‘ ‘。重要特征的缺失值有时会转化成binary处理，但只限于是否缺失为重要信息的特征。一般的缺失值填充有以下方法：

• 数值型特征：可以用 均值/最大值/最小值/众数 填充
• 时间序列特征：例如苹果今天的价格缺失，可以用昨日的价格填充
• 将缺失值归为一类：可以用不曾出现也不会出现的值，比如：缺失年龄用 999 填充，缺失体重用 -1 填充
• 缺失比例小的连续变量：可用有数值的数据进行对缺失值的回归预测填充，例：班上某同学的身高

填充缺失值是没有固定方法的，需要根据不同的应用场景实际判断。

查看相关性

1

df.corr					# 特征之间的相关性

1

sns.heatmap(df.corr(),square=True,annot=True,cmap='YlGnBu') # 也可以用热力图表示

可以发现几个特征之间的相关性特别大，在这个时候，数据的清洗和预处理就更加重要了。由于最后一个变量是房屋的均价，可以把它单独拿出来和其他各个变量做特征，当然也可以在一开始的时候直接使用sns.pairplot(df)来看每个变量之间的相互关系。

1
2
3
4
5
6
7
8
9
10
11
12

plt.style.use({'figure.figsize':(20,25)})
i = 0
for each in df.columns:   
    plt.subplot(5,4,(i+1))
    plt.scatter(df[each],df['MEDV'])
    plt.title(' {} and House price'.format(each))
    plt.xlabel(each)
    plt.ylabel('House Price')
    plt.yticks(range(0,60,5))
    plt.grid()
    i=i+1
plt.show()

用sklearn筛选重要特征

1
2
3
4
5
6
7
8
9
10

drop_columns = ['MEDV']
x = df.drop(drop_columns, axis=1) # 手动划分训练集
y = df['MEDV']
# 用sklearn筛选特征观察
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression # 用回归评测指标
SelectKBest = SelectKBest(f_regression, k=3) # 取前三最相关
bestFeature = SelectKBest.fit_transform(x,y)
SelectKBest.get_support()
x.columns[SelectKBest.get_support()]

SelectKBest的官方源码

输出为Index(['RM', 'PTRATIO', 'LSTAT'], dtype='object')。此时，可以单独对这几个变量做特征，具体做法因项目和实际需要而定，这里不做具体展开。其他用sklearn进行数据处理的方法可参考：sklearn进行特征选择和数据预处理。

模型应用

关于如何对特征进行整合处理，其实有很多做法，例如分箱、独热编码、归一化等等。在这里，只简单套用一下线性回归和随机森林两个模型，跑出结果。

线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 分出数据和标签
X = df.drop(['MEDV'], axis=1).values # 数据
y = df['MEDV'].values # 标签
# 调用模型
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=888)
# 确认训练集和数据集形状
X_train.shape
y_train.shape
# 实例化模型
lin_reg = LinearRegression()
# 训练
lin_reg.fit(X_train,y_train)
# 查看分数
lin_reg.score(X,y) # 0.738792

此时模型已经完成了，可以用lin_reg.coef_查看估计的线性方程系数。也可以用测试集看效果。

1
2
3

from sklearn.metrics import mean_squared_error # 调用均方误差评价指标
y_pre = lin_reg.predict(X_test) # 预测结果
mean_squared_error(y_test, y_pre) # 评价指标 19.10388

随机森林

同样用之前分割好的训练集和测试集，代码不再重写。与线性模型代码不同的是，在这里，使用网格搜索交叉验证的方式充分评估回归模型的准确性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV
# 构造参数字典，让这三个参数按列表中的顺序排列组合遍历一遍
param_grid = {
    'n_estimators':[5,10,20,50,100,200], # 决策树的个数
    'max_depth':[3,5,7], # 最大树深，树太深会造成过拟合
    'max_features':[0.6,0.7,0.8,1] # 决策划分时考虑的最大特征数
}
# 实例化随机森林
rf = RandomForestRegressor()
# 以随机森林为基础构造网格搜索
grid = GridSearchCV(rf, param_grid=param_grid, cv=3)
# 训练
grid.fit(X_train, y_train)

输出结果

1
2
3
4
5
6
7
8
9
10
11

GridSearchCV(cv=3, error_score='raise',
       estimator=RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
           max_features='auto', max_leaf_nodes=None,
           min_impurity_decrease=0.0, min_impurity_split=None,
           min_samples_leaf=1, min_samples_split=2,
           min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
           oob_score=False, random_state=None, verbose=0, warm_start=False),
       fit_params=None, iid=True, n_jobs=1,
       param_grid={'n_estimators': [5, 10, 20, 50, 100, 200], 'max_depth': [3, 5, 7], 'max_features': [0.6, 0.7, 0.8, 1]},
       pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
       scoring=None, verbose=0)

1
2

# 查看效果最好的参数
grid.best_params_

1

{'max_depth': 7, 'max_features': 0.6, 'n_estimators': 100}

1
2
3

# 查看效果最好参数对应的模型
rf_reg = grid.best_estimator_
rf_reg

1
2
3
4
5
6

RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=7,
           max_features=0.6, max_leaf_nodes=None,
           min_impurity_decrease=0.0, min_impurity_split=None,
           min_samples_leaf=1, min_samples_split=2,
           min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=None,
           oob_score=False, random_state=None, verbose=0, warm_start=False)

可视化一下随机森林的预测结果

1
2
3
4
5
6
7
8

result = {"label":y_test,"prediction":rf_reg.predict(X_test)}
result = pd.DataFrame(result)
result['label'].plot(style='k.', figsize=(15,5))
result['prediction'].plot(style='r.')
# 设置可视化图表
plt.legend(fontsize=15,markerscale=3) 
plt.tick_params(labelsize=25)
plt.grid()

1
2
3

from sklearn.metrics import mean_squared_error # 调用均方误差评价指标
MSE = mean_squared_error(y, rf_reg.predict(X))
MSE # 评价指标 4.33319

可以看出随机森林的结果比线性回归预测要好。

这是Datawhale和伯禹学院联合和鲸平台组织的”动手学深度学习“公益学习活动打卡笔记，同时也整理进了一些我平时学习的内容。使用的DIve into DL是pytorch版本，中文网页版链接：https://tangshusen.me/Dive-into-DL-PyTorch/#/

语言处理基础

文本预处理

通常包括四个步骤：

• 读入文本
• 分词（token）
• 建立字典，将每个词映射到一个唯一的索引index
• 将文本从词的序列转换为索引的序列

能较好帮助英文分词的库：spaCy和NLTK。

语言模型

语言模型的目标是为了判断该序列是否合理，即计算该序列的概率。

语言模型（language model）是自然语言处理的重要技术，用它来预测下一个时刻的输出。自然语言处理中最常见的数据是文本数据。我们可以把一段自然语言文本看作一段离散的时间序列。假设序列w1,w2,…,wT中的每个词是依次生成的，则有

为了计算语言模型，我们需要计算词的概率，以及一个词在给定前几个词的情况下的条件概率，即语言模型参数。

n元语法

n元语法通过马尔可夫假设（虽然并不一定成立）简化了语言模型的计算。这里的马尔可夫假设是指一个词的出现只与前面n个词相关，即n阶马尔可夫链（Markov chain of order n）。n元语法是基于n−1阶马尔可夫链的概率语言模型，其中n权衡了计算复杂度和模型准确性。

循环神经网络Recurrent Neural Networks

由于n的增大使模型参数的数量随之呈指数级增长，故引入循环神经网络。

循环神经网络语言模型是一种用于处理序列数据的神经网络。它是一类自带循环的模型，这个循环使得其具备了记忆功能（非长久记忆）。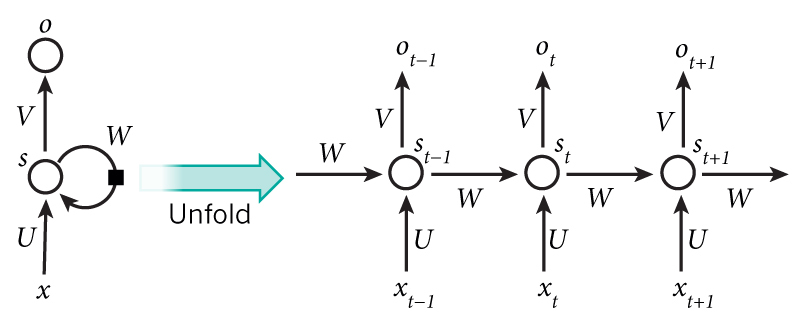

通过BPTT算法训练，“权共享”。

RNN模型种类

• one to many ：生成领域，AI创作小说、音乐
• many to one ：情感分析、舆情监控、听歌识曲、故障监控、声纹识别
• many to many（对齐）：变声（实时）
• many to many（不对齐）：同传、问答系统

  RNN模型的重要变种——LSTM（Long short-term memory)

  LSTM通过“门”来解决RNN网络在长序列训练过程中的梯度消失和梯度爆炸问题。

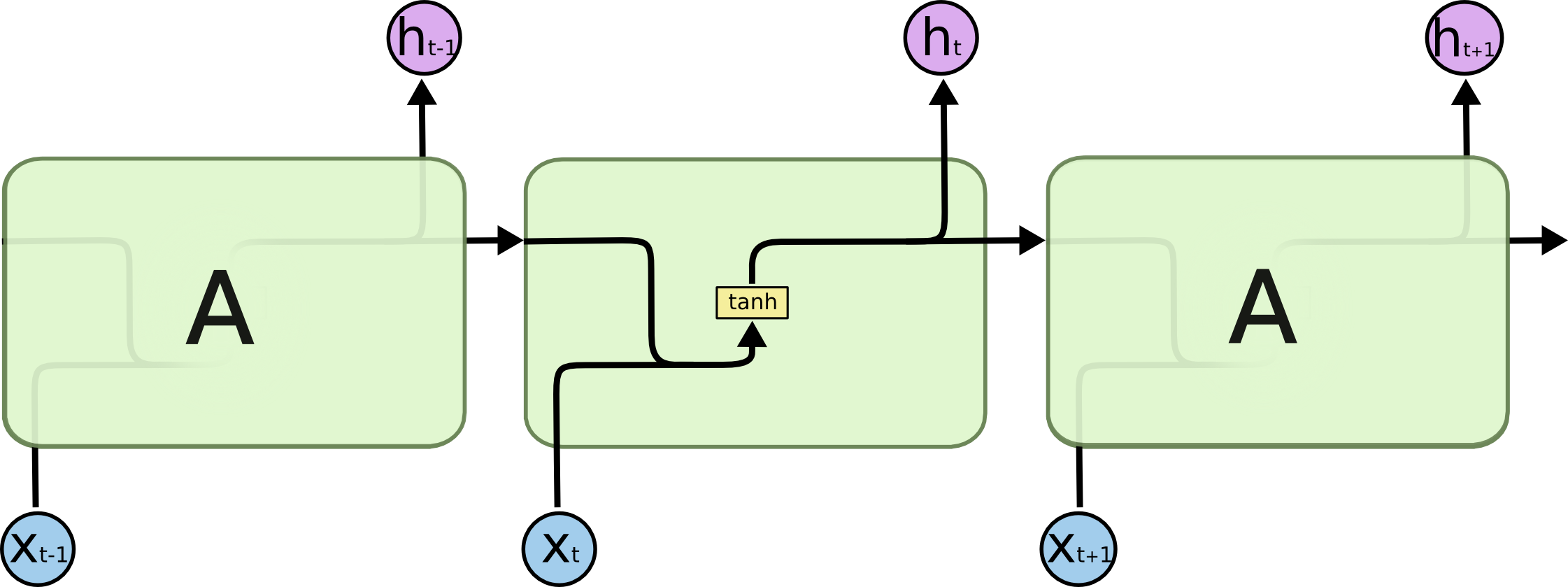
参考：https://colah.github.io/posts/2015-08-Understanding-LSTMs/

LSTM案例：文本生成、命名实体识别

RNN模型的其他变种

深度循环神经网络和双向循环神经网络。

• 深度循环神经网络通过增加隐藏层来实现。
• 双向循环神经网络则是nlp中十分常用的一个模型，它能同时兼顾当前时间前和后的数据信息，例如在文本处理时实现对上下文的联想。

NOT AN END

以上这些可以说只是要了解自然语言处理必须知道的一些基本内容。关于nlp的具体相关算法和思想，如word2vec、nagetive sampling等，有待整理！

这是Datawhale和伯禹学院联合和鲸平台组织的”动手学深度学习“公益学习活动打卡笔记，同时也整理进了一些我平时学习的内容。使用的DIve into DL是pytorch版本，中文网页版链接：https://tangshusen.me/Dive-into-DL-PyTorch/#/

卷积神经网络Convolutional Neural Network

卷积神经网络基本组成

CNN 由于被应用在 ImageNet 等竞赛中而广受欢迎，最近也被应用在自然语言处理和语音识别中。CNN由三部分组成，卷积层、池化层和全连接层。具有三种特性：全值共享、局部连接和下采样（subsampling）。

卷积层

在pytorch中使用nn.Conv2d类来实现二维卷积层

卷积运算

CNN基于二维互相关运算（cross-correlation）。二维互相关运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。下图即为卷积核在卷积时进行的运算。输入Image（即为feature map），黄色矩阵为卷积核（覆盖部分为局部感受野），相乘累加后输出Convolved Frature。

卷积层的超参数

• 填充Padding
  填充（padding）是指在输入高和宽的两侧填充一列或多列元素（通常是0元素）。计算如下图所示。
  

• 步幅Stride
  在互相关运算中，卷积核在输入数组上滑动，每次滑动的行数与列数即是步幅。

多通道卷积

当遇到高维度的数据时（例如彩色图片具有RGB三个通道Channel），输入和输出则为三维数组。例如，当输入具有相当丰富的特征时，需要有多个不同的核数组来提取的是不同的特征。

池化层

在pytorch中使用nn.MaxPool2d实现最大池化层

池化层主要用于缓解卷积层对位置的过度敏感性。同卷积层一样，池化层每次对输入数据的一个固定形状窗口（又称池化窗口）中的元素计算输出，池化层直接计算池化窗口内元素的最大值或者平均值，该运算也分别叫做最大池化或平均池化。

池化的作用：减少参数量、防止过拟合、具有平移不变性（也是CNN具有平移不变性的原因）。

CNN和全连接层（fully connected layers，FC）的简单比较

使用全连接层的局限性：

• 全连接层把图像展平成一个向量，在输入图像上相邻的元素可能因为展平操作不再相邻，故它们构成的模式可能难以被模型识别。
• 对于大尺寸的输入图像，使用全连接层容易导致模型过大。

与全连接层相比，CNN主要有两个优势：

• 卷积层保留输入形状，且具有提取局部信息的能力。
• 卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。

CNN衍生模型发展

LeNet-5 的架构基于这样的观点：（尤其是）图像的特征分布在整张图像上，以及带有可学习参数的卷积是一种用少量参数在多个位置上提取相似特征的有效方式。
由于LeNet在最后使用全连接层，导致计算参数过多，在那时候，没有 GPU 帮助训练，只用CPU很难完成全部的训练。这导致模型最后采用的参数少，神经网络的层数也不多。除了算力以外，当时还有一个很大的限制就是算法领域的研究不够深入，还没有深入研究参数初始化和⾮凸优化算法等诸多领域。

AlexNet

LeNet虽然在1994年被提出，但是在很长一段时间由于算力的限制而没有很好的发挥作用，直到2012年Alex在ImageNet竞赛中提出深度卷积神经网络模型。

AlexNet在LeNet的基础上变得更宽更深了，并且使用了数据增强（Data Augmentation），增大了模型的泛化能力。单纯从网络上来看，它和LeNet的区别体现在：

• 原始数据集的通道数不同。LeNet采用1个通道的灰度图，而AlexNet的数据集是三通道的彩色图像，图像大小也比LeNet大十倍左右。
• AlaxNet的第一层卷积层保持参数数量且之后的池化层均采用最大池化突出图片特征，增加数据的稀疏性。
• 第一次使用ReLU激活函数，避免了使用Sigmoid造成的梯度消失现象。
  AlaxNet采用2个GPU进行训练，在数据处理上也有了更大的能力。当然这只是基础的区别，更详细的算法上的优化有待参考原始论文继续学习。

VGGNet

AlaxNet在模型结果上有了很大的优化，但是没有给后续的实践者一个可以参照的模型或范式继续进行研究。VGG则可以通过重复使⽤简单的基础块（VGG-block）来构建深度模型。

从上图可以看到VGG模型通过增加深度有效地提升性能，并且VGG16的block只有3x3卷积与2x2池化，卷积层保持输入的高和宽不变，而池化层则对其减半。我们可以根据实际样本量的大小选择需要的block比例来进行训练，防止参数过多、样本过少造成的过拟合。

NiN

之前三种网络（LeNet、AlexNet和VGG）都是先以由卷积层构成的模块充分抽取空间特征，再以由全连接层构成的模块来输出分类结果。NiN（Network in Network）则是通过串联多个由卷积层和“全连接”层构成的小⽹络来构建⼀个深层⽹络。该设计后来为 ResNet 和 Inception 等网络模型所借鉴。

• NiN将VGG-block进行了修改，使其变成第二、三层为1×1卷积核卷积的三层卷积层。
• 同时，取消了最后的全连接隐藏层和输出层，改用全局平均池化层来代替（通过在最后一个卷积层改变通道数，使其等于特征数）。

在这里值得一提的是1×1卷积核的作用，如下：

• 放缩通道数，进行卷积核通道数进行降维和升维。
• 1×1卷积核的卷积过程相当于全连接层的计算过程，并且还加入了非线性激活函数，从而可以增加网络的非线性。
• 减少了计算参数。

GoogLeNet

像VGG这样扩大网络规模或增大训练数据集来提高模型的泛化能力可能并不是一个很好的方法，这会带来两个问题：一是网络参数量的急剧增加会导致网络陷入过拟合，尤其是对小数据集而言；二是消耗巨大的计算资源。GoogLeNet是在ImageNet竞赛时提出的，它考虑到VGG的缺点和NiN全连接层的作用，提出了Inception模型。

Inception块相当于⼀个有4条线路的自网络，它通过不同窗口形状的卷积层和最⼤池化层来并⾏抽取信息，并使⽤1×1卷积层减少通道数从而降低模型复杂度。在此模块的基础上，GoogLeNet通过使用22层神经网络和AlexNet一半的参数量完成了自己的模型。

To be continue

这之后，还陆续出现了ResNet和Inception-V4等一些列新模型，等之后几篇再更新。

本次笔记还参考了：从LeNet到GoogLeNet：逐层详解，看卷积神经网络的进化

这是Datawhale和伯禹学院联合和鲸平台组织的”动手学深度学习“公益学习活动打卡笔记。使用的DIve into DL是pytorch版本，中文网页版链接：https://tangshusen.me/Dive-into-DL-PyTorch/#/

数据基础: 张量和梯度

1.张量

Tensor（张量）可以看成是一个多维数组。标量是0维张量，向量是1维张量，矩阵则是2维张量。在深度学习中涉及到大量的矩阵和向量的相互计算（矢量计算的速度更快），在PyTorch中，torch.Tensor是存储和变换数据的主要工具。
除了基本的矩阵向量（同形）的计算之外，对于不同形状的Tensor，会有一个broadcasting机制。即以最大维度的Tensor为基础复制元素，使两个Tensor形状相同。例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

input：
x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)

output:
tensor([[1, 2]])
tensor([[1],
        [2],
        [3]])
tensor([[2, 3],
        [3, 4],
		[4, 5]])

2.梯度

gradient（梯度）在深度学习的过程中经常被使用，其中很重要的就是对函数求梯度，并通过反向传播算法对损失函数进行优化。
需要注意的是，在使用pytorch提供的autograd包执行反向传播的时候，需要将属性.requires_grad设置为True，才能进行计算，否则，这些参数将无法利用链式法则进行梯度计算，也就无法调用.backward()。

基本模型

1.线性回归

线性回归解决连续值的回归问题，属于有监督模型。

线性模型作为深度学习模型中最基础的模型，可以通过对它的学习而触类旁通其他一些回归模型的知识。
它的基本形式为y = ωX + b。
线性回归整个模型流程大致分为读取数据、定义模型、初始化模型参数、定义损失函数（MSE）、定义优化算法和训练模型。

2.softmax回归

与输出连续值的线性回归模型相对，softmax回归输出的是类别这样的离散值。

softmax与线性回归一样，将输入特征与权重做线性叠加，但是它的输出值个数等于标签里的类别数。为了使输出的离散值具有直观意义且可以衡量，在这里使用softmax运算符。它用指数归一化的形式使输出值转化为值为正且和为1的概率分布。
与逻辑回归采用相同的损失函数——交叉熵损失函数。

3.多层感知机

多层感知机相较于线性模型添加了隐藏层，隐藏层和输出层都是全连接层。同时，隐藏层也设置了权重和偏差，将它的表达式带入输出后可以轻易发现联立后的式子依然是一个单层神经网络（仿射变换）。
由此，这里可以引入非线性函数进行变换之后，再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function)。
下面是几种常用的激活函数：

• ReLU（rectified linear unit）
  
• Sigmoid函数
  
• tanh函数（一般用在生成对抗网络和循环神经网络）
  

ReLu函数是一个通用的激活函数，体现在
1）在神经网络层数较多的时候，最好使用ReLu函数，ReLu函数较简单计算量少，而sigmoid和tanh函数计算量则大很多。例如卷积神经网络和全连接神经网络大都使用ReLU。
2）由于梯度消失导致训练收敛速度较慢时，要避免使用sigmoid和tanh函数。
Sigmoid函数除了容易造成梯度消失现象以外，由于它不以零点为中心且函数值一直为正，导致它有zig-zag现象（不同维度的梯度变化方向相同）而使函数的收敛速度变慢。
所以，在选择激活函数的时候可以先选用ReLu函数，如果效果不理想再尝试其他激活函数。
但是，需要注意的是ReLU函数只能在隐藏层中使用。用于分类器时，sigmoid函数及其组合通常效果更好。

过拟合

过拟合指训练误差较低但是泛化误差较大，且二者相差较大的现象。

除了增大数据样本以外，处理多层感知机神经网络的过拟合问题有两种方式：L2范数和丢弃法。

• L2范数
  L2范数正则化也叫权重衰减，它通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制。
• 丢弃法Dropout
  对隐藏层使用丢弃法，即丢弃一定概率该层的隐藏单元，丢弃概率为超参数。

梯度消失、梯度爆炸

当神经网络的层数较多时，模型的数值稳定性容易变差，梯度的计算也容易出现消失或爆炸。

梯度消失的解决办法：

• 使用ReLU激活函数。
• 深度残差网络ResNet。
• 批标准化Batch Normalization。

逻辑回归Logistic Regression

与线性回归不同，逻辑回归不拟合样本分布，而是确定决策边界。决策边界可以是线性，也可以是非线性。

由线性回归引出逻辑回归

在用线性模型处理回归任务时，例如二分类问题，我们通过引入“单位阶跃函数”（红色部分）来产生0/1的判断值。当然，我们希望它是连续的，故采用近似的替代函数——“对数几率函数“（Sigmoid函数）。

实质上，是用线性回归模型的预测结果去逼近真实标记的对数几率，这是一种分类学习方法。

• 它无需事先假设数据分布，避免了假设分布不准确；

• 它不仅仅得到了一个分类标签，更可以得到近似概率预测，对许多需利用概率辅助决策的任务很有用；

• 对率函数是任意阶可导的凸函数，有很好的数学性质。

逻辑回归背后的数学原理 — 极大似然估计Maximun likelihood

似然函数的本质，即选择最佳的参数值w，来最大化样本数据的可能性。同时，为了防止连乘带来的数字下溢，两边同时取对数，得到log可能性函数：

所以，逻辑回归的损失函数

​ S：Sigmoid函数

​ n：训练样本集总数

加上对数之后

由于我们的目标是使似然函数最大，为了计算方便，在等式前加上负号，以求得凸函数的最小值，从而引出了交叉熵（Cross entropy）损失函数。

只有一个样本的情况下，函数可以拆解为

由此可得，当y=1时，样本概率越接近1损失函数越小；当y=0时，样本概率越接近0损失函数越小。

部分参考：https://blog.csdn.net/xlinsist/article/details/51289825